Improving FP16/16 matmul accuracy with two-stage accumulation

On Nvidia consumer GPUs such as the RTX 4090, FP16/32 matrix multiplication is limited to run at half the speed of FP16/16, meaning users need to choose between either using tensor core operations that accumulate in FP16 precision or only getting 50% of the GPU’s peak performance.

We can improve the accuracy of FP16/16 matrix multiplication with a two-stage accumulation strategy: use FP16/16 tensor core mma instructions but accumulate the results outside the mma in separate FP32 registers.

This is done by changing the main loop of the matmul kernel from

for (int k=0; k < K; K += K_BLOCK) {
  // load global->shared->reg etc.
  // ...
  mma_m16n8k16(aReg, bReg, dReg, dReg);
  __syncthreads();
}

to (simplified for clarity)

unsigned cReg[2] = {0};
for (int k=0; k < K; K += K_BLOCK) {
  // load global->shared->reg etc.
  // ...
  dRegPtr = reinterpret_cast<half *>(dReg);
  mma_m16n8k16(aReg, bReg, cReg, dReg);
  dRegAcc[0] += __half2float(dRegPtr[0]);
  dRegAcc[1] += __half2float(dRegPtr[1]);
  dRegAcc[2] += __half2float(dRegPtr[2]);
  dRegAcc[3] += __half2float(dRegPtr[3]);
  __syncthreads();
}

The full code is available in Kernel 3.2 here.

An alternative approach to maintaining separate FP32 accumulator registers in the main loop would be to use Split/Stream-K and convert to FP32 when accumulating partial results.

Performance

We look at the performance impact on one problem shape: M=N=K=4096, using normally distributed inputs ¹. Benchmarking setup as described in my previous post on Ada matmuls.

On this problem shape, the two-stage accumulation kernel achieves 209.1 TFLOP/s, which is 79% of cuBLAS FP16/16 performance.

Kernel	Execution Time	TFLOP/s	% 4090 peak FP16/16
cublasGemmEx FP16/32	895 us	153.6	47.5%
Two-stage accumulation	657 us	209.1	63.3%
cublasGemmEx FP16/16	520 us	264.2	80.0%

Accuracy

We compare the results of each kernel to a reference kernel that computes the matmul using FP32 operations on CUDA cores. Percentiles of absolute error of each kernel compared to this reference are shown in the plot below.

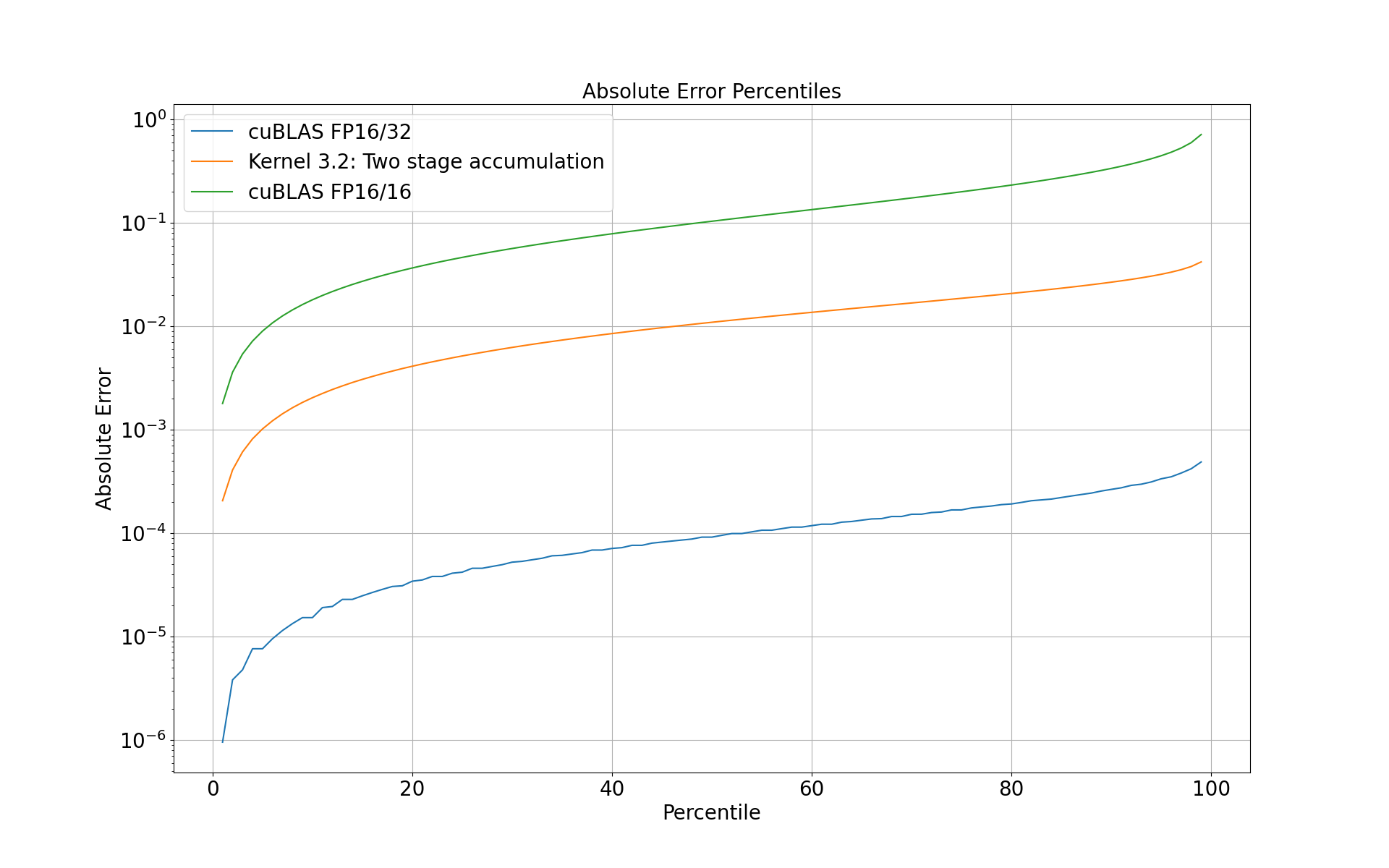
Roughly speaking the two-stage accumulation kernel has ~100x larger absolute error than cuBLAS FP16/32, and ~10x smaller absoluter error than cuBLAS FP16/16.

So the two-stage kernel is 36% faster than cuBlAS FP16/32 but with ~100x larger absolute error, as compared to cuBLAS FP16/16 which is 72% faster with ~1000x the absolute error.

References

1. As discussed in great detail on Horace He’s blog, the distribution of input data has a noticeable impact on performance. ↩

 
Author Sam Patterson. Licensed under a CC BY 4.0 License.